Eratosthenes
(276-196 B.C.)
Compiled and illustrated by D. Newsome
-Nicknamed “Beta” [second to whom, I don’t know… perhaps Aristotle???
-He is generally described as having been the “head of the library at Alexandria” What it means to be a head librarian in an ancient library is hard to tell. I imagine he was sort of a resident researcher.
His claim to eternal fame… He calculated the circumference of the earth.
How he did it…
Idealized version first….
1. On the summer solstice, at noon, the apogee of the sun’s motion in relation to the horizon, he observed that there was no shadow of a perfectly vertical pole at Syene, which I am locating at 23.9ľ N in order to make the math as clean as possible.
2. At noon, a vertical pole at Alexandria, located by me for easy math at 31.1ľN, casts a shadow amounting to 7.2ľ.
3. Recall Euclid…
4. Eratosthenes knew that Syene was 5000 stades from Alexandria.
5. Do the math…
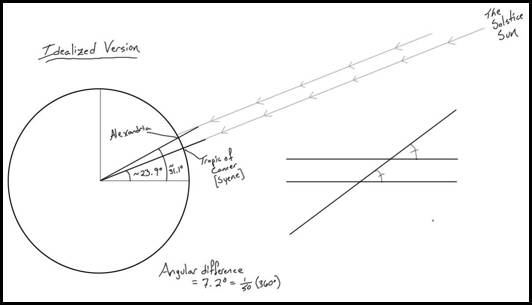
The math gives you 25,000 stades around. We’ll look at stades in a minute.
Eratosthenes’ assumptions and measurements:
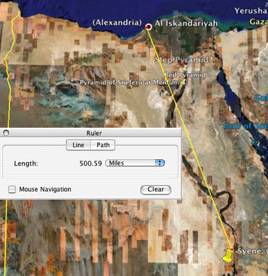
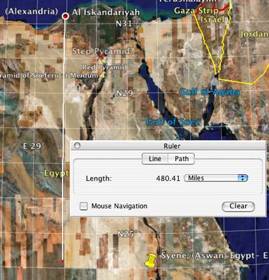
1) Distance from Alexandria to Syene was 5,000 stades. It seems that he is assuming that Syene and Alexandria are on the same meridian (constant longitude), which they are not. This doesn’t have to matter so long as it is factored into the final answer. Judging from this GoogleEarth experiment, the latitudinal distance is 96% of the actual distance. So we may want to keep that in mind when we get final results.
2) Sun rays are, for all practical purposes, parallel. The assumption here is that the sun is really, really far away.
3) A line intersecting parallel lines has equal alternate angles. [Euclid]
4) The shadow cast was 1/50 of a circle, or 7.2ľ
Now here are some nitty gritty details that make the
calculation a bit messier.
Eratosthenes noticed that at midday, the sun at its
apogee, of the solstice at
Syene (almost at the Tropic of Cancer, from bet. 24ľ07’N to about 23ľ52’N, One source claims 23ľ26’)
(actually 60 km north and not quite on the same meridian) a vertical rod (or
well) casts no shadow. Tropic of Cancer is 23ľ27’N.
In Alexandria (bet 31ľ05’N and 31ľ17’N) (to the north of
Syene (modern Aswan)) on the same day a vertical rod always cast a shadow. The minimum shadow cast (when the sun
at its apogee) was determined to be 1/50 of a circle, 7.2ľ. On summer solstice the sun will be
directly overhead.
The difference range is from 7ľ10’ to 7ľ25’. That is 7.16667ľ to 7.41667ľ, which yields 1/50.23 to
1/48.21.
The result is that he figured the circumference to be 250,000 stades.
The next big question…
What is a stade? or stadia? …or stadium? I have found many answers to this question. It’s a bit like asking what the distance to right field is in baseball.
1 mile = 7.5 stades approx.
1 stade = 157m = 0.1333 miles approx. = 515 ft.
1 stade = 185
meters (607 feet) [this one gets lots of votes]
also have seen the stade to be
1 stade = 600 = 183m
and
1 stade = 500 ft. = 152m
also saw
1 stade = 528 ft. = 161m, which makes 10 stadia = 5280 ft = 1 mile. Thus 5000 stadia = 500 miles.
…track at Olympia measures 210 yards (630 ft.)
from N.M.U web site
1
stade=177.6 m (Attic-Roman)=185 m
(Std. Roman)=192 m (Olympic)=197.3 m
(Philetaeran).
So,
the stade estimates range from 152m (500ft.) to 197.3m (647ft.) … that’s a 30% increase from 152.
Modern circumference numbers 24,901.55 miles (40,075.16 kilometers).
If a stade is the low estimate… that gives a result of 38,000km (5.2% low error)
If a stade is the high estimate… that gives a result of 49,325km (23% high error)
If we want a stade estimate that cheats to the modern circum,
use the stade = 160.3m = 526ft. (0% error)
Earlier estimates for the circumference of the earth:
Eudoxus of Cnidus (d. ca. 355 B.C.) 400,000 stades
Dicaearchus (student of Aristotle) 300,000 stades
Aristarchus of Samos (d. 230 B.C.) 300,000 stades
A later librarian of Alexandria, Ptolemy, ….His estimate was 180,000 stadia (about 28,800 km.) (about 28% low)
Combined with this was a popular belief in the late 15th c. that Asia was wider than it really is due to trying to incorporate Marco Polo’s descriptions of Japan…(Wilford, p. 61) and …
…Columbus was expecting Asia to be a quick trip.
Many reasons for Columbus’s voyage usually stated as “God, gold, and glory.” : economic (spices), exploration, conquest, imperial ambitions…
The “God” reason is more interesting that it at first seems. Why would God be a reason? He wrote to his benefactors Ferdinand and Isabella that he wanted to find a quick root to the Orient (East, China, India, etc.) in order to facilitate the conversion of those non-Christians into good Catholic people. What’s the rush? Time was running out. Columbus believed that the end-of-days was going to happen in 155 years. The world was going to be destroyed and saved all at the same time. But in order for this to happen, all on the earth had to be converted to Christianity. Columbus was on a mission of God, missionizing the peoples of the earth in the “last days.” He called himself “Christo-ferens.” [Christ-bearing]
Where did he get this figure, 155 years? The end was going to come in the 1650s.
He got this number in the same place he got his circumference of the earth figure, in a book by Pierre d’Ailly (1350-1420). It was a book on geography and astrology and the end of the world. D’Ailly later revised his date to 1789 (the French Revolution coincidentally).
Cheating historians of science from the Web:
Circumference = 50 x 5000 stades = 250,000 stades
250,000 stades x 157 meters/stade = 39,250 kilometers
The modern value: 40,070 kilometers.
This is a difference of only 2%!!
Ptolemy made a similar geometric estimate based on stellar (rather than solar) measurements made earlier by Marinus of Tyre (by way of Posidonius). This value gave a circumference of 28,800 kilometers. This is 72% of the correct value.
By about 300AD, the idea of a Flat Earth was revived:
Early Christian rejection of the "pagan absurdity" of a spherical earth.
This view was held sporadically until about 1300 AD.
By 1300, the works of Ptolemy and others arrived in Europe by way of Islamic Spain, and fully restored the Spherical Earth to respectability.
Contrary to popular myth, few educated people after about 300 BC doubted that the Earth was a sphere. While a few early Christian thinkers did try to reject the idea, there is nothing in Christian beliefs that dictates a Flat Earth, in fact is says nothing at all on the matter.
Eratosthenes' work was lost, except for a description of his method in an obscure source (Cleomedes Meteora, written around 370 AD). (I think Martianus Cappella also mentions it….)
Ptolemy's estimate survived in his influential writings on geography. An interesting consequence of this transmission was:
It makes the eastern tip of Asia closer to the western tip of Europe than it would be otherwise.
This fact (along with some other finagling) convinced Columbus that he might be able to reach Japan by sailing West from the Canaries.
Unlike many others of his time, however, Columbus not only argued for a smaller Earth, he also convinced the Spanish government to provide him the means to put his claims to the test.